
ТОР 5 статей:
Методические подходы к анализу финансового состояния предприятия
Проблема периодизации русской литературы ХХ века. Краткая характеристика второй половины ХХ века
Характеристика шлифовальных кругов и ее маркировка
Служебные части речи. Предлог. Союз. Частицы
КАТЕГОРИИ:
- Археология
- Архитектура
- Астрономия
- Аудит
- Биология
- Ботаника
- Бухгалтерский учёт
- Войное дело
- Генетика
- География
- Геология
- Дизайн
- Искусство
- История
- Кино
- Кулинария
- Культура
- Литература
- Математика
- Медицина
- Металлургия
- Мифология
- Музыка
- Психология
- Религия
- Спорт
- Строительство
- Техника
- Транспорт
- Туризм
- Усадьба
- Физика
- Фотография
- Химия
- Экология
- Электричество
- Электроника
- Энергетика
Несобственные интегралы
Понятие несобственного интеграла является обобщением понятия определенного интеграла на случай, когда либо подынтегральная функция обращается в бесконечность, либо промежуток интегрирования бесконечен.
Пусть функция f(x) задана на [  ] и интегрируема на любом сегменте [
] и интегрируема на любом сегменте [  ] при
] при  >
>  . Если предел интеграла
. Если предел интеграла

при  существует, то его будем называть несобственным интегралом от функции f(x) в пределах от
существует, то его будем называть несобственным интегралом от функции f(x) в пределах от  до
до 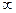 и обозначать символом
и обозначать символом


Приведем достаточный признак существования несобственного интеграла- признак сравнения: если 

 при
при 
 x<
x<  и существует несобственный интеграл
и существует несобственный интеграл  то существует также несобственный интеграл
то существует также несобственный интеграл  Поэтому существует предел интеграла
Поэтому существует предел интеграла 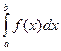 при
при 
Пример 6. Найти несобственный интеграл 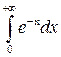 .
.
Решение. По определению
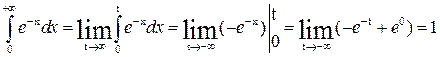 ,
,
т.е. несобственный интеграл сходится к 1.
Пример. Покажем, что интеграл  сходится при
сходится при  >0. Воспользуемся интегрированием по частям:
>0. Воспользуемся интегрированием по частям:

Первое слагаемое в правой части равенства имеет предел при x  а интеграл
а интеграл
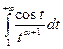 сходится на основании признака сравнения, так как
сходится на основании признака сравнения, так как 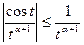 и интеграл
и интеграл  сходится. Следовательно, существует предел интеграла
сходится. Следовательно, существует предел интеграла 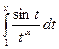 при x
при x  .
.
Пример 7. Вычислить несобственный интеграл  .
.
Решение. По определению ([3], c.382)
 ,так как вычисленный
,так как вычисленный
интеграл при 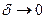 стремится к пределу 2, то несобственный интеграл
стремится к пределу 2, то несобственный интеграл  сходится.
сходится.
Тема 3
Двойной интеграл [1, гл.III]
Рассмотрим на нескольких примерах приемы вычисления двойных интегралов.
Пример 8. Вычислить повторный интеграл 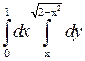 , затем изменить порядок интегрирования, вычислить полученный интеграл и сравнить ответы.
, затем изменить порядок интегрирования, вычислить полученный интеграл и сравнить ответы.
Решение.
а) 
б) Строим область интегрирования (заштрихованная рис.1) согласно заданным пределам по x и по y и меняем порядок интегрирования.Эту область разобъем отрезком прямой y=1 (x 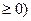 на две замкнутые области D
на две замкнутые области D  . В D
. В D 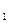 y изменяется от 0 до 1, а x изменяется от 0 до y. В D
y изменяется от 0 до 1, а x изменяется от 0 до y. В D 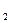 имеем 1
имеем 1  . Окончательно поучим:
. Окончательно поучим:


Рис.1
Пример 9. Вычислить двойной интеграл 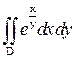 по области
по области
 .
.
Решение. Представим двойной интеграл в виде повторного: сначала по х, затем по у (рис.2)

Рис. 2

Интеграл  найдём по частям.
найдём по частям.
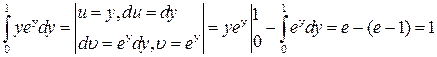
Интеграл  . Поэтому
. Поэтому  .
.
Тема 4 [4,гл.XIII]
Не нашли, что искали? Воспользуйтесь поиском: